房间内有 100 人，每人有 100 块，每分钟随机给另一个人 1 块，最后这个房间内的财富分布怎样？

N人共有M元的情况下：

1. 最终的分布是 在标准(N-1)-单纯形(Simplex)上 边长为M的格点上的随机游走(Random walk) 的稳态分布 的各分量的分布；
2. 随机游走相当于求解离散空间的热传导方程(Heat equation)；
3. 在一定条件下，稳态分布近似单纯形上的均匀分布——对称狄利克雷分布(Dirichlet distribution)，其分量服从指数分布(Exponential distribution)。

注：以下是每分钟「某个人」给另一个人钱的情况，而不是每分钟（还有钱的）「每个人」给另一个人钱情况。请注意这两者的区别，详细见评论。

====================

一个极重要的隐含假设是，我们不允许负债。令x_i表示第i个人的钱数，则所有的可行状态在以下空间内：

x_1+...+x_N=M, \quad where \quad x_i\in \{0,...,M\}, i\in\{1,...,N\}

这是一个边长（一个顶点到另一个顶点的格点数）为M的(N-1)-单纯形上的所有整数点。

（注意一般地标准单纯形的定义是在实空间上的，是内部的所有实数点。在这里我们盗用了这个术语...）

易知状态的总数为C(M+N-1, N-1)。当N=100，M=100*100 时（100人每人100元），状态总数的量级在10^240的级别。直接求解几乎不可能..

例如，当有3人每人有2元（共6元）时，状态空间是边长为6的2-单纯形（正三角）上的所有整数点。

当初始状态为绝对平均的 (222) 时，随时间变化相当于以该点为起始 在这个空间上的无偏随机游走。

====================

这样的随机游走理论上是可以得到稳态的。考虑一个简单的2人各2元的情况，状态空间为 (40), (31), (22), (13), (04)；状态转移矩阵为

\begin{bmatrix} 0 & .5 \\ 1&0&.5\\ & .5 & 0 & .5 \\ &&.5 & 0 & 1 \\ &&& .5 & 0 \end{bmatrix}

易得稳态分布为[1,2,2,2,1]/8。

直观上，在除了边界的区域上分布应该是均匀的。（未证明）

但由上述，状态空间极大，钱数多时像这样直接求解十分困难。

====================

一般地，令p_n(x)为时间为n时状态为x的概率，定义格点上的算子Δ如下

\Delta p(x)=\sum_{y:d(x,y)=1}[p(y)-p(x)]

其中d(x,y)是两点之间的距离。d(x,y)=1 表示x和y是相邻的，可以从一点转移到另一点。

则状态转移方程可以写为

\frac{\partial p_n(x)}{\partial n} = \alpha \Delta p_n(x)

其中α控制转移的速度。

有没有发现和热传导方程有点像？

\frac{\partial u}{\partial t} = \alpha \nabla^2u

其实上述定义的Δ算子就是图上的离散Laplacian (Discrete Laplace operator)，方程是图上的离散热传导方程。随机游走的稳态分布可以近似看作是热传导的终态。（未证明）

====================

====A HUGE GAP=====

====================

注意到 M钱数多->格点密集，N人数多->单纯形维数高。

我们考虑在某种条件下，以连续热传导方程近似格点上的随机游走。进一步地，忽略对边界上的讨论，将终态视为单纯形上的均匀分布。（未证明）

（注意这里有一个极大的gap，我们未严格讨论在什么情况能用连续Laplace算子代替图上的Laplacian）

User:Skinnerd/Simplex Point Picking 这里讨论了如何在单纯形上随机取样或模拟随机游走。注意到单纯形上的均匀分布相当于参数α=(1,1,...,1)的狄利克雷分布，其分量服从指数分布（？）。具体地：

x_i \sim Exponential(1), S = \sum x_i, t_i=\frac{x_i}{S} \quad (i=1,...,N)

则t_i是标准N-单纯形上的均匀分布。

====================

若上述成立，500人各500元时最终大概会变成这样子：

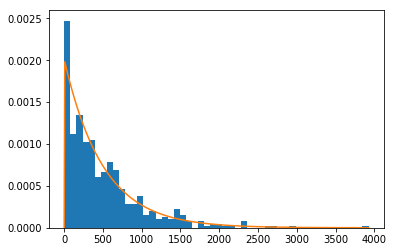
此外我们注意到，当N变大时，单纯形维数高，由于维数灾难，大部分点是在“边角”处的。

N-单纯形的体积是\frac{1}{n!}\sqrt{\frac{n+1}{2^n}}

单纯形的中心（最均匀的分布）距离最近的边界（其中1人为0其他人均匀分布）的距离是\sqrt\frac{1}{2n(n+1)}

单纯形内接球在单纯形中的占比为

也就是说，人数超过10人时，经过一定时间的交换，几乎一定至少有一个人“破产”。

====================

这篇回答只是提供一个可能的方向，如何联系随机游走和热方程。充满了大大小小的gap，但我并没有时间深究了。我找到了这本书：

[1] G. F. Lawler, “Random Walk and the Heat Equation.”

看起来蛮有趣的。希望有读者能够解释一下如何严密地联系离散时间离散状态和连续时间连续状态，在什么情况下可以近似，以及如何随时间变化等等。欢迎讨论。

不需要那么多物理假设, 纯粹的数学解法也能给出显式解.

整个过程应该分为两个阶段,第一个阶段是有人破产前,第二个阶段有人破产后.

无破产模型

假如大家都非常有钱, 那么短时间内就不会破产

所以这个阶段等价于无破产模型

取32人做10000次交易操作,做一个排序:

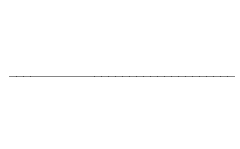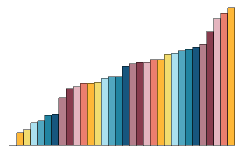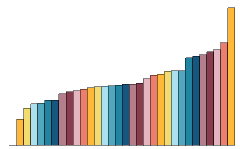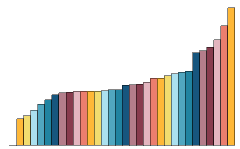
好像不太明显...来1K个人交易100K次看看:

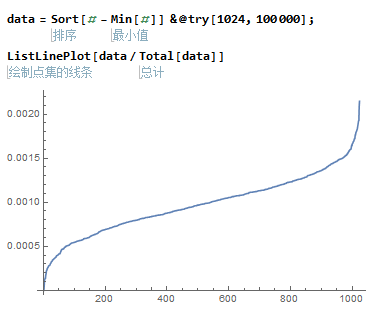
这个曲线的解析表达式是什么呢?

无偏随机游走

假如人很多,那么每个人就可以近似的看成随机游走.

这个是 @王赟 Maigo 的想法

每个人得到钱的期望是1元,自己每回合又要给别人1元,所以这就是无偏随机游走

无偏随机游走的距离随时间成二项分布.

二项分布是正态分布的离散化,人很多(n>12)用正态分布替代也无妨.

也就是说用财富划分区间,然后统计人数之后的分布近似是正态分布.

排序在这当中起了什么作用呢?

排序相当于是求次序统计量(OD)的逆累计分布函数(ICD).

统计学上有个专门的叫法: q分位数

很多知友很有数学直觉,认为这个结果必定是由于某种量的累积.

然后归结于随机算法的误差...

这就说不过去了, 蒙特卡罗法是现代工程的支柱,以大数律为担保.

@灵剑 一针见血的指出了这是由于方差的累积

事实上也确实如此

无偏随机游走的均值不会改变,开始是100,不管多少时间之后还是100.

但是方差却不断地累积,方差与时间平方成正比.

引证: 随机游走中,怎么理解最终行走距离的平方的期望等于步数？

所以最终这条曲线的解析表达式就是:

f(q)=\mu -\sqrt{2t} \ \text{erfc}_{-1}\left(\frac{2 q}{\text{N}}\right)

其中 t 是经过的时间, \mu 是开始时的总金额, N 是总人数

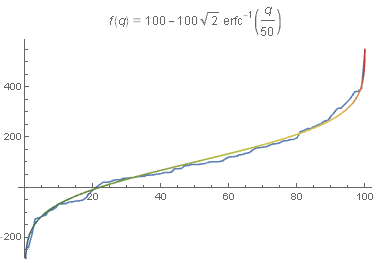
第一个破产者出现在 t=\frac{\mu ^2}{2 \text{erfc}_{-1}\left(\frac{2}{\text{N}^2}\right)^2}\approx 1287 回合时.

带反射壁的随机游走

接下来就是 @张雨萌 的思路:

破产者接下来还是随机游走---带反射壁的随机游走

从原点出发,可以使用镜像法研究

从原点 (0,0) 出发经过 (n,v) 的概率是:

P_n(v)=\binom{n}{\frac{1}{2}(n+v)}p^\frac{1}{2}(n+v)q^\frac{1}{2}(n-v)

然后我们把起始点从 (0,0) 移动到(0,\mu) 处

P_n(v)=\binom{n}{\frac{1}{2}(n+v-\mu)}p^\frac{1}{2}(n+v-\mu)q^\frac{1}{2}(n-v+\mu)

令 p=q=\frac{1}{2} , 当 n 很大时, 服从韦伯分布

P_n\sim\mathrm{Weibull}(\alpha,\mu,0) , \alpha 为需估计参数,与 n,\mu 都相关.

引证: https://arxiv.org/pdf/math/0603208.pdf

韦伯分布的经典用途就是寿命估计

对于人类来说, 出现致命意外概率一开始比较小,后面会变大, 然后最后可能趋于一个常数,按照这个模型可以精确地估计人类寿命分布.

这个模型也是这样, 一开始有破产风险的人没有,然后有一点点, 最后稳态的时候趋于一个常数.

但是上有破产风险的人只占一小部分,实际上无穷多人的话这部分人的测度为 0.

所以可以近似为无衰减韦伯分布,即 \alpha \approx1 , 也就是所谓的指数分布.

q\sim\mathrm{Weibull}(1,\mu,0)=\mathrm{Exp}(1/\mu)\quad \mu为初始金额

所以最终稳态时曲线的解析表达式就是

f(q)=-\mu \log \left(1-\frac{q}{\text{N}}\right)

综上所述:

房间内有 100 人,每人有 100 块,每分钟随机给另一个人 1 块,最终财富曲线就是 f(q)=-100 \ln \left(1-\frac{q}{100}\right)

为了消去奇点, 每个人左平移半格比较合适.
q=100 时理论解是无穷大, Exciting...

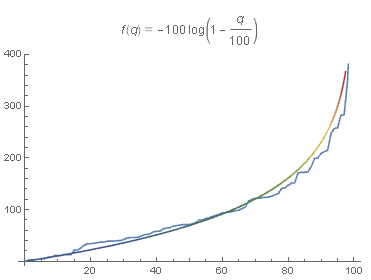
PS: 好像物理方法估出来是玻尔兹曼分布?
我查了下玻尔兹曼分布,发现似乎和韦伯分布差不多?
从最大熵分布的角度上看:
玻尔兹曼的熵约束是: {\displaystyle \operatorname {E} (x^{2})=3a^{2},\,\operatorname {E} (\ln(x))\!=\!1\!+\!\ln \left({\frac {a}{\sqrt {2}}}\right)\!-\!{\frac {\gamma _{\mathrm {E} }}{2}}}
韦伯分布的熵约束是: {\displaystyle \operatorname {E} (x^{k})=\lambda ^{k},\operatorname {E} (\ln(x))=\ln(\lambda )-{\frac {\gamma _{\mathrm {E} }}{k}}\,}

不平等度

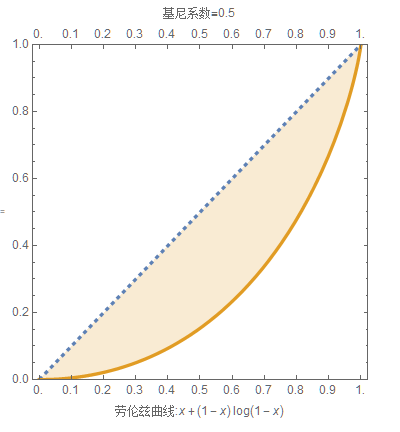
不平等度可以用劳伦兹曲线来研究.

如果累积分布函数为 F(t),t>0 ,那么有:

劳伦兹曲线: L(x)=\frac {1}{\mu }\int_0^x F_{-1}(t)\ \mathrm{d}t

指数分布 \mathrm{Exp}(1/\mu) 的CDF为 F(t)=1-e^{-\frac{t}{\mu }} .

所以劳伦兹曲线为 L(x)=x+(1-x) \log (1-x) ,与人数和时间都无关.

所谓基尼系数就是均等曲线与劳伦兹曲线围成的面积(黄色部分)与三角形的比值

基尼系数: G={\frac {1}{\mu }}\int _{0}^{\infty }F(t)(1-F(t))\ \mathrm{d}t, 算得基尼系数恒为 0.5

人生经验

随机造就了幸运儿, 随机也会造就流浪汉...

人人都在随机游走,人的命运不可预料.....

如果你是个聪明人, 能比别人看的更准 1^\circ ,那你至少能进入上层.

如果你是个冒险者, 你愿意付出双倍代价,去获取双倍回报.

那么在第一种社会中很容易破产, 但是在第二个福利社会中十有八九是人生赢家.

如果你一贫如洗,那就只能随波逐流,如果你本就是人生赢家,那有可能赢者通吃...

当然, 时间的力量是神奇的, 任何人都可能触底, 任何人也都可以走上人生巅峰...